IN CASE OF EMERGENCY CALL 911
Note: This page is a list of quick reference tools to help with knowledge of crash investigations! Your use of Crash Math is "FREE".
The information within Crash Math is in all attempts, accurate, and the results of any formula should be verified. In other words considered correct, but unless you have checked and/or done the math yourself and qualified the information provided yourself in that nothing on this page is implied as expert testimony, nor implied as evidentiary, for litigation, or any other form of court use, and by no means a official report.
**PLEASE ENJOY AND CHECK THE ANSWERS - DO THE MATH! Recommend a Scientific Calculator or a good cell phone App.
Message from Author - Hello and Hope All is Well. So, there are many other formulas or Expressions involved within the subject matter that this tool helps with. These formulas or expression are not explained nor represented. In taking the Advanced Crash Investigation to further my understanding and knowledge of this subject in order to apply lessons taught while on the job. It is strongly recommend one must continue on their own and recommend at a pace comfortable to that person and revisit the subject matter of the course frequently. Creating this tool is a method of furthering the understanding of the math of Advanced Crash Investigation by other applicable means.
THIS TOOL IS ALWAYS A WORK IN PROGRESS!
Order of Operations and Mentions:
The order of operations is a rule that tells the correct sequence of steps for evaluating a math expression.
We can remember the order using P.E.M.D.A.S.: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
☝ More info - Click to see More in or Examples
Example
SMph. = √30D'f ± 1
D' = 120' and f = .8
Note: 30Df ±1 could look like (30Df ±1) or 30 * D * f ±1
SMph. = √30 * 120' * 0.8 ± 1
Ok, so we need to do the Multiplication first, and we determined 1 is a negative integer -1
☝ - More info!
Applying (-) Negative and or (+) Positive Integers (Numbers).
What if, we have to apply a negative integer to a positive integer?
We need to subtract the negative integer from the positive integer:
- 1 ← Negative Integer + 1 ← Positive Integer = 0
- 1 ← Negative Integer + 2 ← Positive Integer + .5 ← Positive Integer = 1.5 ← Positive Integer
What if we have to apply a negative integer to a negative integer?
We need to add negative integers and the result is a negative integer:
- 1 ← Negative Integer + - 1 ← Negative Integer = - 2 ← Negative Integer.
- 1 ← Negative Integer + - 2 ← Negative Integer + -.05 ← Negative Integer = -3.05 ← Negative Integer.
SMph. = √2880 -1
We subtracted 1 or added -1
SMph. = √ 2879
Then the radical √ = square root
SMph. = 53.65631370118525
Now we need to round off to the hundredths, so we get 53.66 Mph.
☝ - More info!
☝ Click image to enlarge
Consider this, It is not necessary to know any derivation by heart, but it is
necessary to know or have a very good understanding of what we are doing. When we apply our work to a profession environment (I.e. Court), remember we must do our work correctly (In other words; Check, check, and check again, then get someone else to check, check, and check again!), show the math, and clearly display our method used in getting our results in our explanation.
Consider this, We need to and should take note of a conversion factor that we will use in nearly every formula derivation.
That is the number 1.466. This number is found by dividing the number of feet in a mile = 5280 feet' by the total number of seconds in an hour 3600 seconds(sec.). The result gives us 1.4666666, which we will to 1.466.
Note: We do not round any further and must us this result as is and 1.466 is used to convert (Feet per Second)fps. into (Miles Per Hour)Mph. or vice versa. As an example: 60 Mph. times 1.466 equals 88 fps. or 88 fps. divided by 1.466 equals 60 Mph..
We see Velocity (Vfps.), which is in fps., is replaced by (SMph. x 1.466), which changes to fps. to Mph. and we have not altered the equations.
Consider this, we will see 1.6 which = 1.6 seconds(sec.) 1.6 secs. is a representation of a average reaction time that we as humans have when we have no other external or internal impeding stimulus effecting us.
If we don't remember any other thing, it is imperative that we remember this mention. If you don't understand it, contact someone who does and get some assistant and better understanding.
Ke = .05(M)V2 is the formula for energy in motion
Consider this, We we see the numerical value 30 mentioned in expressions, 30 is a derivative. What are Derivatives? They are the result of performing a differentiation process upon a function or an expression. Derivative notation is the way we express derivatives mathematically.
Legend (Key):
″ = Symbol for unit of measure Inches.
′ = Symbol for unit of measure Feet.
Ke = .05(M)V2 Kinetic Energy formula for energy of motion.
D = Distance in feet.
S = Speed in miles per hour (Mph.).
V = Velocity in feet per second (fps.).
f = Drag factor (Coefficient of Friction).
f = Coefficients
☚ More info.
fAdj = Adjust Drag factor (Coefficient of Friction) adjusted.
t = Time (In Seconds ≡ Sec.).
R = Radius (Feet ').
C = Chord (Feet ').
g = Acceleration of gravity or 32.22
feet per second squared (32.22 fps.).
RAdj = Radius (Adjusted) (Feet ').
H = Height (Feet ').
Sc = Combined Speed (Mph.).
W = Weight (lbs.) = How much gravity is pulling down on an object.
n = % Breaking Efficiency.
n = Breaking Efficiency
☚ More info.
Vehicle Drag Factor fAdj =μ (% weight) (n)
M = Mass = How much matter is contained within an object.
of an object divided by the acceleration of gravity or W/g.
30 = A constant that arises in the process of the derivation.
15 = ½ of the constant of 30 that arose in the process of the derivation.
1.466 = A conversion factor: 5280 '/3600 sec. in a hour.
1.6 sec. = A normal average reaction time in seconds.
μ = Coefficient of Friction on Level Surface
Note: Here for a level surface μ = f.
e = Road Grade elevation 2% would be converted to .02
Se = Super elevation 2% would be converted to .02
Se = Super-elevation
☚ More info.
Super-elevation = Se = e = h/D
Vo = Original Velocity (fps.).
Possible Coefficients of Friction for Various Roadway(Surfaces)
Note: The values shown in this table are for information purposes only. They provide a starting point for the investigator to determine, through proper testing, the actual coefficient of friction for the surface(s) the investigator is concerned with.
Well Worn
Smoother from use
New, Fresh Surface
Dry
.50 -.75
.60 - .75
.70 - 1.20
Wet
.35 -.60
.45 - .70
.50 - .60
Excess Tar
Bleeding
Well Worn
Smoother from use
New, Fresh Surface
Dry
.35 - .60
.45 - .75
.55 - .80
.65 - 1.20
Wet
.25 - .55
.40 - .66
.40 - .65
.45 - .80
Loose
Packed, Well Traveled
.10 - .25
.05 - .10
Snow
Loose
Packed on Road
Penetration of Snow Bank
Penetration Avalanche
.10 - .25
.25 - .25
(Colder usually higher)
Approximately .50
1.50 - 3.00
.30 - .50
.30 - .60
Note: On pavement or packed gravel, a free rolling tire on an automobile will have a deceleration factor of about .20 per tire. A rolling wheel on a powered axle will have a deceleration factor of about .03 in high gear per tire.
Other Drag Factors (Approximate)
Large Animals on pavement:
.70
Steel on pavement or packed gravel:
.40
Aluminum on pavement or packed gravel:
.45 - .50
People on pavement sliding:
.60 - .90
People tumbling on pavement or other surface:
1.00
Street Motorcycle sliding with light scratching:
.30 - .35
Motorcycle with crash bars:
.20 - .40
Motorcycle with significant pavement scratches:
.50 - .60
Motorcycle on soil (use lower value for harder soil, higher value for soft soil, may tumble):
.70 - 1.20
Rollovers (from last pavement mark to end)
(higher value represent more real world):
.40 - .65
Deceleration in Critical speed yaw:
.00 - .30
.40 - .60
.60 - .80
.90 - 1.50
Note: These values are based on the experience of a large number of complete investigations. If in doubt, TEST THE PROBLEM YOURSELF
Expressions:
μ = F ÷ W
Find μ (Coefficient of Friction)
×
F = Kinetic Energy (Force) Ke = .05(M)V:
F =
W = lbs.
RESULT:
μ = F ÷ W
μ = ÷
Calculate
f = μ ± m
Grade Adjustment Expression: f = μ ± m
×
μ - Coefficient Friction (See Chart)
Note: m = Uphill or Positive Grade(Elevation) DO NOT ADD - BEFORE INTEGER.
- m = Down Hill or Negative Grade(Elevation) ADD - BEFORE INTEGER.
If level LEAVE EMPTY
KNOWNS:
μ =
m =
RESULT:
f = μ ± m
f = ±
Calculate
Snow
Loose
Packed on Road
Penetration of Snow Bank
Penetration Avalanche
.10 - .25
.25 - .25
(Colder usually higher)
Approximately .50
1.50 - 3.00
.30 - .50
.30 - .60
Note: On pavement or packed gravel, a free rolling tire on an automobile will have a deceleration factor of about .20 per tire. A rolling wheel on a powered axle will have a deceleration factor of about .03 in high gear per tire.
Other Drag Factors (Approximate)
Large Animals on pavement:
.70
Steel on pavement or packed gravel:
.40
Aluminum on pavement or packed gravel:
.45 - .50
People on pavement sliding:
.60 - .90
People tumbling on pavement or other surface:
1.00
Street Motorcycle sliding with light scratching:
.30 - .35
Motorcycle with crash bars:
.20 - .40
Motorcycle with significant pavement scratches:
.50 - .60
Motorcycle on soil (use lower value for harder soil, higher value for soft soil, may tumble):
.70 - 1.20
Rollovers (from last pavement mark to end)
(higher value represent more real world):
.40 - .65
Deceleration in Critical speed yaw:
.00 - .30
.40 - .60
.60 - .80
.90 - 1.50
Note: These values are based on the experience of a large number of complete investigations. If in doubt, TEST THE PROBLEM YOURSELF
☝ More info!
Example
Click Image to enlarge
← Open image in separate window
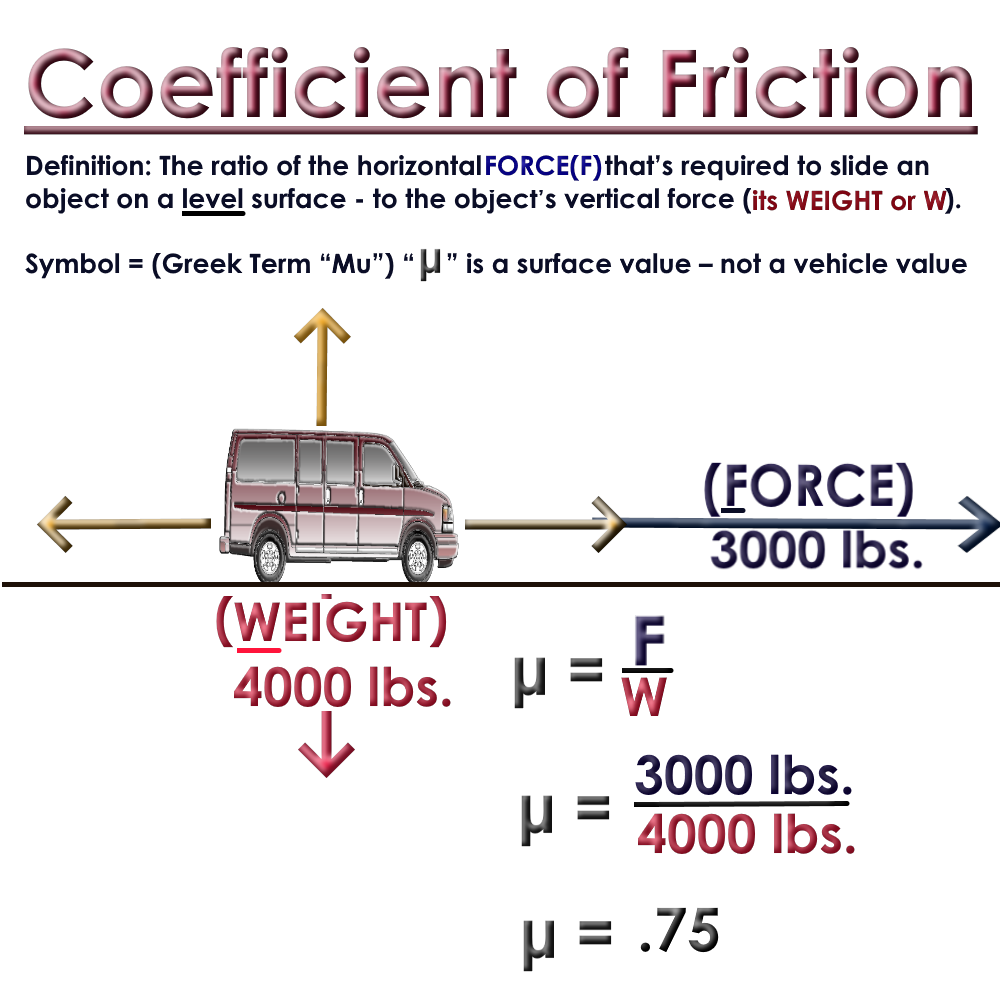
We know that a vehicle skidding downhill will have a reduced(-) less coefficient of friction and a vehicle skidding uphill will have a greater(+) more coefficient of friction.
Consider this, A mini van crash takes place where the road surface is Asphalt and we have a 2% downhill grade.
Using our f = Coefficients Asphalt (Well Worn) has a Coefficient of Friction range of .45 - .75. Giving the benefit to the operator (Note: Use the higher decimal) We determined the Coefficient of Friction (μ) is .75 with a Downhill grade of 2%.
f = µ ± m← Will Work!
KNOWNS DOWNHILL:
µ = .75
f = -.02
RESULT:
f = µ ± m
f = .75 ± -.02 ← Downhill Grade we use negative(subtract).
f = 0.73
KNOWNS UPHILL:
µ = .75
f = -.02
RESULT:
f = µ ± m
f = .75 ± +.02 ← uphill Grade we use positive(add).
f = 0.77
Click image to enlarge
← Open image in separate window
Special Note: Finding f = μ ± m like other formulas listed are derived from a more complex algebraic formulas. Being familiar with these other formulas could help you visualize the mathematical progression.
fAdj = fLF + fRF + fLR + fRR
Snow
Loose
Packed on Road
Penetration of Snow Bank
Penetration Avalanche
.10 - .25
.25 - .25
(Colder usually higher)
Approximately .50
1.50 - 3.00
.30 - .50
.30 - .60
Note: On pavement or packed gravel, a free rolling tire on an automobile will have a deceleration factor of about .20 per tire. A rolling wheel on a powered axle will have a deceleration factor of about .03 in high gear per tire.
Other Drag Factors (Approximate)
Large Animals on pavement:
.70
Steel on pavement or packed gravel:
.40
Aluminum on pavement or packed gravel:
.45 - .50
People on pavement sliding:
.60 - .90
People tumbling on pavement or other surface:
1.00
Street Motorcycle sliding with light scratching:
.30 - .35
Motorcycle with crash bars:
.20 - .40
Motorcycle with significant pavement scratches:
.50 - .60
Motorcycle on soil (use lower value for harder soil, higher value for soft soil, may tumble):
.70 - 1.20
Rollovers (from last pavement mark to end)
(higher value represent more real world):
.40 - .65
Deceleration in Critical speed yaw:
.00 - .30
.40 - .60
.60 - .80
.90 - 1.50
Note: These values are based on the experience of a large number of complete investigations. If in doubt, TEST THE PROBLEM YOURSELF
☝ More info.
Click image to enlarge
← Open image in separate window
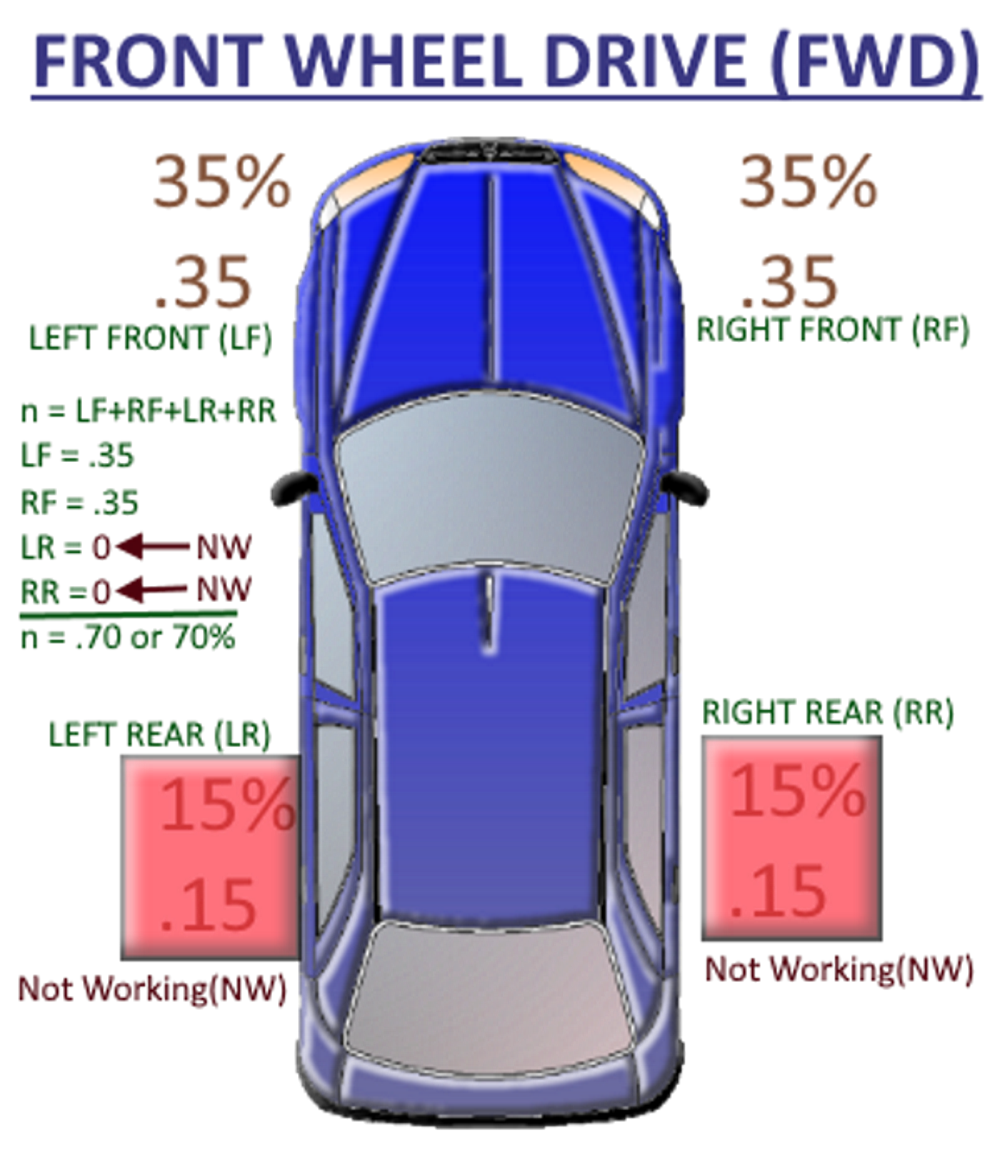
We said the vehicle is FRONT WHEEL DRIVE (FWD) and according to Breaking Efficiency diagram above the LEFT FRONT(LF) tire provides 35% = .35 of the vehicles breaking and the RIGHT FRONT (RF) tire provides 35% = .35 of our vehicle's breaking, and the two rear tires (LR, RR) each provide 15% = .15, but the two rear breaks were Not Working(NW), so they are providing no breaking or 0% = .0.
So, we add 35% = .35 for the LEFT FRONT(LF) tire, 35% = .35 for the RIGHT FRONT(RF) tire, 0% = .0 for the LEFT REAR(LR) tire, and 0% = .0 for the RIGHT REAR(RR) tire.
(n) = Total Breaking Percentage or our vehicles Breaking Efficiency is 70% = .70
Special Note: Finding D = Skid Distance (D) like other formulas listed are derived from a more complex algebraic formulas. Being familiar with these other formulas could help you visualize the mathematical progression.
Snow
Loose
Packed on Road
Penetration of Snow Bank
Penetration Avalanche
.10 - .25
.25 - .25
(Colder usually higher)
Approximately .50
1.50 - 3.00
.30 - .50
.30 - .60
Note: On pavement or packed gravel, a free rolling tire on an automobile will have a deceleration factor of about .20 per tire. A rolling wheel on a powered axle will have a deceleration factor of about .03 in high gear per tire.
Other Drag Factors (Approximate)
Large Animals on pavement:
.70
Steel on pavement or packed gravel:
.40
Aluminum on pavement or packed gravel:
.45 - .50
People on pavement sliding:
.60 - .90
People tumbling on pavement or other surface:
1.00
Street Motorcycle sliding with light scratching:
.30 - .35
Motorcycle with crash bars:
.20 - .40
Motorcycle with significant pavement scratches:
.50 - .60
Motorcycle on soil (use lower value for harder soil, higher value for soft soil, may tumble):
.70 - 1.20
Rollovers (from last pavement mark to end)
(higher value represent more real world):
.40 - .65
Deceleration in Critical speed yaw:
.00 - .30
.40 - .60
.60 - .80
.90 - 1.50
Note: These values are based on the experience of a large number of complete investigations. If in doubt, TEST THE PROBLEM YOURSELF
☝ More info.
Click image to enlarge
← Open image in separate window
← Open image in separate window
Special Note: Finding f = μn ± m like other formulas listed are derived from a more complex algebraic formulas. Being familiar with these other formulas could help you visualize the mathematical progression.
Snow
Loose
Packed on Road
Penetration of Snow Bank
Penetration Avalanche
.10 - .25
.25 - .25
(Colder usually higher)
Approximately .50
1.50 - 3.00
.30 - .50
.30 - .60
Note: On pavement or packed gravel, a free rolling tire on an automobile will have a deceleration factor of about .20 per tire. A rolling wheel on a powered axle will have a deceleration factor of about .03 in high gear per tire.
Other Drag Factors (Approximate)
Large Animals on pavement:
.70
Steel on pavement or packed gravel:
.40
Aluminum on pavement or packed gravel:
.45 - .50
People on pavement sliding:
.60 - .90
People tumbling on pavement or other surface:
1.00
Street Motorcycle sliding with light scratching:
.30 - .35
Motorcycle with crash bars:
.20 - .40
Motorcycle with significant pavement scratches:
.50 - .60
Motorcycle on soil (use lower value for harder soil, higher value for soft soil, may tumble):
.70 - 1.20
Rollovers (from last pavement mark to end)
(higher value represent more real world):
.40 - .65
Deceleration in Critical speed yaw:
.00 - .30
.40 - .60
.60 - .80
.90 - 1.50
Note: These values are based on the experience of a large number of complete investigations. If in doubt, TEST THE PROBLEM YOURSELF
☚ More info.
So...We have a vehicle that ends up in a collision with a another motor vehicle, we have four measured skid marks in feet', the vehicle's speed is constant, and the road's grade and/or super elevation appears level.
f = S2 / 30(D) will work.
Example
Click image to enlarge
← Open image in separate window
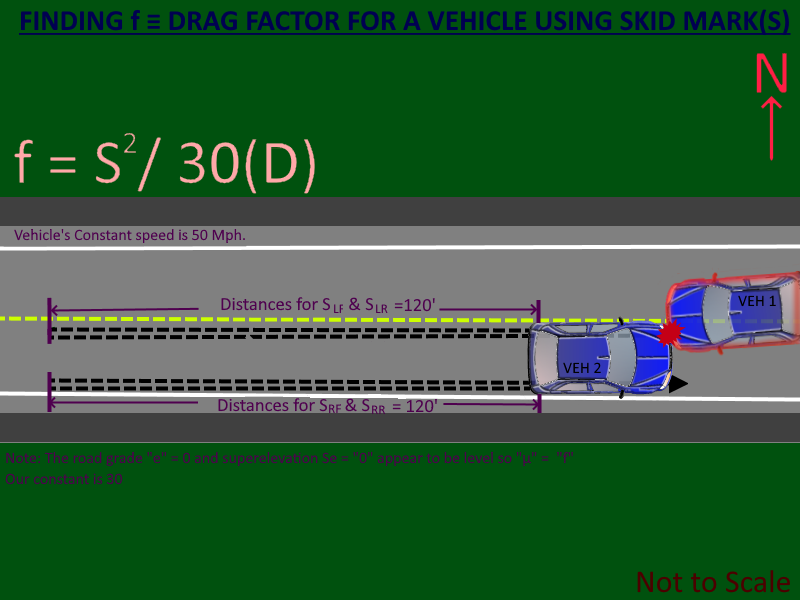
So, We need to determine the Coefficient of Friction or the Drag Factor f.
We assume the speed of the vehicle is constant at 50 Mph. We've measured the measured the (Left Front Tire)SLF skid mark @ 120', the (Left Rear Tire)SLR skid mark @ 120', the (Right Front Tire)SRF skid mark @ 120', and the (Right Rear Tire)SRR skid mark @ 120'.
We get the average distance of the skid marks in feet DAvg' by getting the sum of all 4 skid mark distances SLF' + SLR' + SRF' + SRR' and then dividing the result by the number of skid marks (4) and we get an average measured Distance (D) of 120 feet'. Since all four tires were locked and skidding we have determined a 100% breaking efficiency and our road grade and super-elevation are "0".
DAvg.' = SLF + SLR + SRF + SRR / Number of Skid Marks measured.
DAvg'.DAvg.' = D = 120'
f = S
2 / 30(D')
f = 50
2 Mph / 30(120')
f = 2500' / 3600'
f = 0.694
Note" we don't have a unit of measure for (f).
Special Note: Finding the f = Factor from skid marks like other formulas listed are derived from a more complex algebraic formulas. Being familiar with other formulas like the derivation of the minimum speed formula could help you visualize the mathematical progression.
.
Last updated on (UTC-5/EST-Eastern Standard Time): May, 05-24-2022 10:28:36 AM.